Сущность метода
Триангуляция заключается в определении пространственного местоположения специально закрепленных на местности геодезических пунктов в вершинах целого ряда треугольников. Изначально, с высокой степенью точности (до долей секунд) определяют азимуты исходных направлений ab, ba, mn, nm (рис.1.Триангуляционный ряд треугольников по меридиану).
Следующим этапом будет определение астрономических координат (широты и долготы) в пунктах измерений азимутов двух исходных базисов. В каждой паре жестких сторон (ab, mn) координаты измеряются только в одной точке, например a,m (рис.1). При этом следует обратить особое внимание на определение астрономических широт в ряду треугольников, расположенных по направлению меридианов. При измерениях в треугольниках, сформированных вдоль параллелей, необходимо уделить должное внимание определению астрономических долгот. Далее производят измерения длин двух базисных сторон (ab, mn).
Эти стороны имеют сравнительно не большие длины (порядка 8-10 км). Поэтому их измерения более экономичные и точные относительно сторон cd, tq, составляющих расстояния от 30 до 40 км. В следующую очередь выполняется переход от базисов ab, mn через угловые измерения в ромбах abcd и mntq к сторонам cd, tq. А затем последовательно практически в каждой вершине треугольников cde, def, efg и других измеряются горизонтальные углы до примыкания к следующей основной стороне tq всего ряда треугольников.
Через измеренные углы треугольника с измеренной базисной или вычисленной основной стороной последовательно вычисляются все другие стороны, их азимуты и координаты вершин треугольников.
Виды триангуляции
Триангуляция данных.
Источники данных могут являться объектами триангуляции, и исследователь должен стремиться к применению как можно большего количества источников, оказавшихся в его распоряжении. Но, по мнению Дензина, должно существовать понимание того, что существует различие меж источниками, при помощи которых исследователь получил какие-либо данные, и методиками сбора информации.
Временная триангуляция.
Всякое социологическое исследование в стиле «кейс стади» производится, как правило, не за один день, а растянуто во времени. С точки зрения времени очень интересным является то, как определенные разновидности деятельности приобретают изменения со временем. Временная триангуляция дает возможность отследить, какие процессы являются неизменными с течением времени, какие кардинально меняются, какие попросту исчезают.
Пространственная триангуляция.
Традиционно исследование «кейс стади» касается сложных объектов, с многоуровневой управленческой системой. В таких исследованиях необходимо собирать данные на различных уровнях организации. В этом исследователям помогает пространственная триангуляция, подразумевающая сбор данных на различных уровнях изучаемого объекта.
Исследовательская триангуляция.
Чем большее число исследователей привлекается к изучению какого-либо случая, тем более достоверной и менее искаженной будет получена информация. Анализ должен отражать логику фактов, а не особенности их восприятия исследователем, зачастую обусловленные его личностным мировоззрением, его опытом. Итоги анализа одного и того же интервью различными исследователями должны являться более или менее схожи, но это не означает необходимости поиска полного согласия в их интерпретации.
Теоретическая триангуляция.
Линкольн и Дензин советует развить концептуальные модели с позиции теоретической триангуляцией, что обозначает подход к данным с разных теоретических направлений и с многими гипотезами в голове. Когда одна из теорий исчерпает себя, можно привлекать следующую для обоснования фактов, которые оставались необъясненными.
Это наиболее сложная разновидность триангуляции. Вести порекомендовал базовые шаги процедуры теоретической триангуляции, являющиеся актуальными и сейчас:
- Сформируйте все возможные предположения, которые имеют право на существование в такой сфере;
- Дайте всевозможные интерпретации по всем выдвигаемым предположениям;
- Предпринимаемое исследование производится с целью определения, какие из этих гипотетических явлений есть на эмпирическом уровне.
- Те предположения, что провалились с треском при ведении исследования, – отбросьте в корзину, как и интерпретации, обладающие с ними связью.
- Наиболее удачные из предположений отбираются в процессе следующих эмпирических наблюдений.
- В заключение сформулируйте список тех предположений, прошедших проверку и тех, что провалились, делая переоценку тех теорий, из которых они проистекли.
- Обозначьте измененную теоретическую систему, которая основана на всех точках рассмотрения и эмпирических подтверждениях, которые вы обрели только что.
Преимущества теоретической триангуляции.
- Во-первых, теоретическая триангуляция минимизирует вероятности того, что исследователь будет предоставлять миру и самому себе недостаточно зрелые предположения, в границах которых какие-то противоречия будут игнорированы.
- Во-вторых, –возможность применять самые широкие обобщения.
- В-третьих, – триангуляция поощряет системную преемственность в исследованиях и теории.
Методологическая триангуляция.
Эта разновидность триангуляции бывает двух разновидностей:
- Внутриметодный;
- Межметодный.
Внутриметодная триангуляция является триангуляцией, когда исследователь применяет лишь одну методику, но внутри этой методики использует множественные стратегии для работы с данными. Межметодная триангуляция является использованием нескольких исследовательских методик так, что одна методика усиливает другую.
К вышеописанным видам триангуляции можно также добавлять и триангуляцию респондентов, подразумевающую давать возможность респондентам оценивать основные итоги исследования.
Итак, мы дали описание ставшим уже классическими видам триангуляции. В практической жизни их необходимо применять в разнообразном сочетании.
Триангуляционные сети
После первого применения градусного измерения дуги Снеллиусом триангуляционный метод становится основным способом в геодезических высокоточных измерениях. С XIX века, когда триангуляционные работы стали более совершенными с его помощью стали формироваться целые геодезические сети, строящиеся вдоль параллелей и меридианов. Самая знаменитая из всех известна под наименованием геодезической меридианной дуги Струве и Теннера (1816-1852) в последствие зачислена в мировое наследие по ЮНЕСКО. Ее триангуляционный ряд протянулся по Норвегии, Швеции, Финляндии и России от Северного Ледовитого океана до Черного моря в устье Дуная и составил дугу в 25º20´.
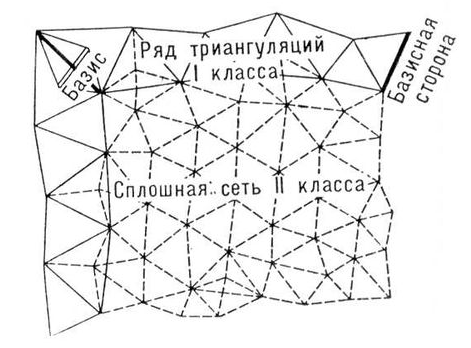
За основу геодезических сетей триангуляции в нашей стране принята схема профессора Ф.Н.Красовского. Ее суть заключается в применении принципа построений от общего к частному. Изначально закладываются вдоль меридианов и параллелей пункты, образующие ряды треугольников протяженностью в пределах 200-240 км. Длины сторон в самих треугольниках составляют 25-40км. Все астрономические измерения азимутов, координат (широт и долгот) выходных точек на пунктах Лапласа и промежуточных астрономических точках, высокоточные базисные геодезические измерения и в каждой точке этой цепи должно соответствовать установленным требованиям I класса точности. Замкнутый полигон из четырех триангуляционных рядов представляет собой фигуру, напоминающую квадрат с периметром равным ориентировочно около 800 км. Через центральные части первоклассных рядов триангуляции устраиваются в направлении друг к другу основные ряды триангуляционной сети II класса соответствующей точности. Базисные длины сторон в этих рядах не измеряются, а принимаются базисы со сторон триангуляции I класса. Аналогично отсутствуют и астрономические пункты. Возникшие четыре пространства заполняются сплошными триангуляционными сетями и II, и III классов.
Безусловно описанная схема развития сетей триангуляции по Красовскому не может закрыть всю территорию страны ввиду понятных причин больших лесных и не заселенных территорий страны. Поэтому с запада на восток вдоль параллелей были проложены отдельные ряды первоклассной триангуляции и полигонометрии, а не сплошная триангуляционная сеть.
Описание алгоритма
Идея заметающей прямой заключается в том, что все точки сортируются по одному направлению, а затем по очереди обрабатываются.
- Отсортируем все точки вдоль некоторой прямой (для простоты по координате ).
- Построим треугольник на первых 3 точках.
Далее для каждой следующей точки будем выполнять шаги, сохраняющие инвариант, что имеется триангуляция Делоне для уже добавленных точек и, соответственно, МВО для них. - Добавим треугольники, образованные видимыми ребрами и самой точкой (то есть добавим ребра из рассматриваемой точки во все концы видимых ребер).
- Проверим на условие Делоне все четырехугольники, порожденные видимыми ребрами. Если где-то условие не выполнилось, то перестроим триангуляцию в четырехугольнике (напоминаю, что их всего две) и рекурсивно запустим проверку для четырехугольников, порожденных ребрами текущего четырехугольника (ибо только в них после изменения условие Делоне могло нарушиться).
Замечание: в шаге при рекурсивном запуске можно не проверять четырехугольники, порожденные ребрами, исходящими из рассматриваемой на данной итерации точки (их всегда два из четырех). Чаще всего они будут невыпуклыми, для выпуклых доказательство чисто геометрическое, оставлю его на читателя. Далее будем считать, что выполняется только 2 рекурсивных запуска на каждое перестроение.
Видимые точки и видимые ребра
Пусть задана минимальная выпуклая оболочка (далее МВО) конечного множества точек (ребра, соединяющие некоторые из точек так, чтобы они образовывали многоугольник, содержащий все точки множества) и точка A, лежащая вне оболочки. Тогда точка плоскости называется видимой для точки А, если отрезок, соединяющий ее с точкой А, не пересекает МВО.
Ребро МВО называется видимым для точки А, если его концы видимы для А.
На следующей картинке красным помечены ребра, видимые для красной точки:
Замечание: контур триангуляции Делоне является МВО для точек, на которых построена.
Замечание 2: в алгоритме видимые для добавляемой точки А ребра образуют цепочку, то есть несколько подряд идущих ребер МВО
Хранение триангуляции в памяти
Есть некоторые стандартные способы, неплохо описанные в книге Скворцова. Ввиду специфики алгоритма, я предложу свой вариант. Так как хочется проверять 4-угольники на условие Делоне, то рассмотрим их строение. Каждый 4-угольник в триангуляции представляет из себя 2 треугольника, имеющих общее ребро. У каждого ребра есть ровно 2 треугольника, прилегающих к нему. Таким образом, каждый четырехугольник в триангуляции порождается ребром и двумя вершинами, находящимися напротив ребра в прилегающих треугольниках.
Так как по ребру и двум вершинам восстанавливаются два треугольника и их смежность, то по всем таким структурам мы сможем восстановить триангуляцию. Соответственно предлагается хранить ребро с двумя вершинами в множестве и выполнять поиск по ребру (упорядоченной паре вершин).
Телефон в режиме ожидания
Базовые станции регулярно передают сигналы в эфир, чтобы телефоны могли понимать, находятся ли они в зоне покрытия. Телефоны же, напротив, большую часть времени ничего не передают, только принимают, с целью экономии заряда батарей. Это легко проверить на практике, положив телефон рядом с компьютерными аудиоколонками и наблюдая за наводимыми телефоном возмущениями либо купив простейший брелок-детектор GSM-сигналов. Отсюда следует, что определить местоположение обычного GSM-телефона в обычной GSM-сети в произвольный момент времени нельзя просто потому, что телефон молчит и никому «не сообщает», где он и куда его несут.
Да, периодически телефон уведомляет сеть о том, в каком месте он находится, чтобы упростить доставку входящих звонков. Происходит это:
- при регистрации в сети;
- при переходе абонента из зоны покрытия одной группы базовых станций в другую (в группу может входить несколько сотен базовых станций, на миллионный город может быть всего дюжина подобных групп);
- периодически — раз в полчаса-час, в зависимости от настроек сети.
При этом телефон сообщает сети только о том, какую базовую станцию он «слышит» лучше всего, без всяких подробностей вроде уровня сигнала и т.п. Базовые станции не следят за тем, какие телефоны находятся в зоне их покрытия, это бессмысленно и технически неосуществимо. Соответственно, у мобильной сети большую часть времени есть лишь весьма приблизительные сведения о том, где сейчас обитает телефон. Может ли при этом стандартная мобильная сеть заниматься измерением расстояния до телефона, не выводя его из режима ожидания?
Во-первых, непонятно, от какой базовой станции измерять — со времени последнего обновления информации о местоположении телефон могли унести на значительное расстояние. Во-вторых, непонятно, что и как измерять. Базовая станция — не радиолокатор, и если телефон «молчит», то для нее он не существует.
Итак, в режиме ожидания стандартный телефон в стандартной сети GSM полностью невидим для мобильной сети и не может быть ею «триангулирован».
Сам телефон при этом находится в более выигрышном положении. Дело в том, что каждая базовая станция транслирует в эфир информацию о своих «соседях», указывая частоты, на которых работают ближайшие базовые станции той же сети. Телефон в режиме ожидания постоянно измеряет уровень сигнала (но не затухание) от каждой из «соседних» базовых и при необходимости выбирает в качестве дежурной базовой станции ту, сигнал от которой «лучше слышно».
Если телефон обладает какими-то сведениями о том, где (по каким координатам) расположены базовые станции, то он может попытаться вычислить зону, в которой области гипотетического покрытия всех «соседних» базовых пересекаются. Где-то в пределах этой области и будет находиться телефон. Чем точнее телефон знает (или оценивает) границы зон покрытия, тем точнее будет работать такой метод. По имеющейся информации, именно так работает приложение Google Latitude. Если же данных о местонахождении базовых станций нет, то и у телефона не будет никакой возможности «триангулировать» свое положение.
Телефон в активном режиме
В активном режиме телефон посылает сигналы какой-то одной базовой станции и принимает от нее ответные сигналы.
У всех на слуху тот факт, что сети GSM могут работать на частотах 900, 1800 и (реже) 1900 mHz. На самом деле речь идет о диапазонах частот:890-960, 1710-1880 и 1850-1990 mHz соответственно.
Каждая базовая станция вещает только на одной определенной частоте из этого диапазона. Соседние базовые станции, независимо от того, какому оператору они принадлежат, всегда конфигурируются так, чтобы создавать друг другу минимум помех. В частности, соседние базовые станции никогда не будут работать на одной и той же частоте.
Базовая станция в процессе обслуживания разговора выполняет контролирующие и регулирующие функции. Она занимается расчетом величин так называемого временного сдвига (timing advance) и передает их телефону. Телефон использует их, чтобы корректировать ход своего таймера так, чтобы у него и у базовой станции «часы» шли синхронно и посланные телефоном сигналы достигали базовую станцию в пределах отведенного телефону «окна вещания». Чтобы правильно рассчитать временной сдвиг, базовая станция измеряет время прохождения сигнала от себя до телефона, но ей абсолютно не важно, сколько раз по пути следования сигнал отразился от зданий и прочих препятствий. Базовая станция также оценивает уровень сигнала от телефона и степень его затухания и выдает телефону рекомендации по необходимой мощности передачи.
Телефон в процессе разговора тоже имеет информацию о временном сдвиге, уровне сигнала от базовой станции и мощности своего передатчика. Получается, что и базовая станция, и телефон могут, в принципе, как-то оценить расстояние друг до друга по пути следования радиосигнала, но они никак не могут учесть все возможные преломления и отклонения. Точность измерения расстояния по временному сдвигу составляет примерно 500 м.
Выводы
Если не вести речь про какого-то конкретного оператора, а говорить о GSM как о технологии вообще, то можно утверждать, что:
- Стандартные возможности сети GSM допускают построение систем определения местоположения абонента на основании измерения параметров прохождения радиосигнала, но стандарта GSM Phase 2+ на такие системы/технологии нет.
- Если в сети оператора не внедрена подобная технология, то средствами самой сети можно определить только последнее известное местоположение абонента с точностью до базовой станции, которая обслужила его звонок или регистрацию в сети. Можно послать на телефон SMS или позвонить и актуализировать эту информацию.
- На базе стандартного телефона сети GSM можно построить систему определения его местоположения, но только в том случае, если доступны данные о координатах установки базовых станций.
- Способ определения местоположения телефона средствами сети при помощи триангуляции (в том виде, в котором он изложен в начале статьи) — не более чем расхожий вымысел.
- https://geostart.ru/post/317
- https://spravochnick.ru/sociologiya/sociologicheskie_issledovaniya/triangulyaciya_v_sociologicheskom_issledovanii/
- https://habr.com/ru/post/445048/
- https://mobile-review.com/articles/2009/triangulation.shtml